Con todas las dificultades que supone la toma de datos fiables en las circunstancias en las que nos encontramos, se dispone de una serie diaria homogénea de número de afectados por el virus a partir del 14 de marzo, cuando desde las distintas administraciones se cambia el método de conteo, sin que se haya vuelto a comunicar ningún cambio metodológico de momento. En esa serie de datos lo que se observa es que, a partir del día 26 de marzo, el número de nuevos casos empieza a desacelerar (fig. 1), lo cuál, sobre todo, son muy buenas noticias, pero además nos permite hacer algunos cálculos para conocer de forma aproximada la duración de esta crisis y el número de afectados totales cuando todo acabe.
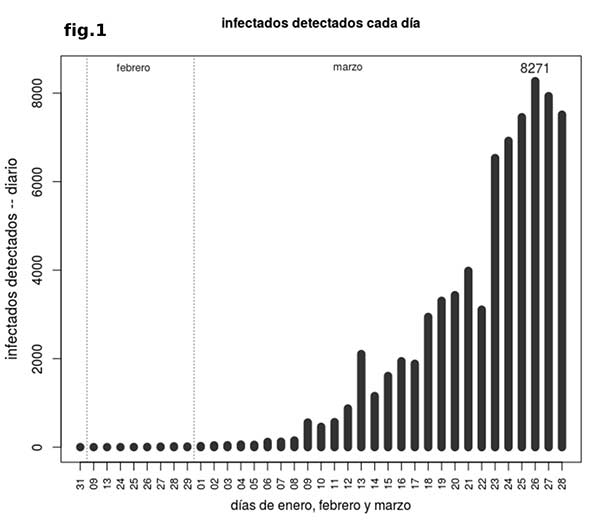
La modelización de un brote epidémico como éste en el que nos encontramos se puede realizar a partir de distintas variables de seguimiento y modelos teóricos que las replican y permiten proyecciones en el tiempo. Si utilizamos el número de casos totales desde que empezó la epidemia (número de casos acumulados, fig. 2), se puede ajustar a ellos un modelo logístico o algunas de sus variantes, como la función de Gompertz, por ejemplo. En ambos casos se asume un número total de infectados finales, cuando la epidemia termine, que suele denominarse por la letra K. Para calcular esa K es necesario saber el momento en el que el número de casos diarios empieza a disminuir, que es el que se alcanzó hace dos días (pico). En el modelo logístico, K es igual al doble del número de casos acumulados cuando se alcanza el pico de casos diarios. En el modelo de Gompertz, K es igual a los casos acumulados en el pico multiplicados por 2.72 (el número e). El pico de casos diarios se alcanzó, si los datos de días venideros no lo desmienten, el pasado 26/03/2020, con 57786 infectados detectados en España hasta ese momento desde que se inició la epidemia (primer caso detectado: 31 de enero). Por tanto, podemos calcular que el número total de infectados detectados cuando todo acabe puede estar en la horquilla K=115572 y K=157079 según consideremos crecimiento logístico o de Gompertz respectivamente. Como la mortalidad respecto a infectados detectados en este momento es del 8.17%, si extrapolamos podemos calcular que el número de fallecidos al final de la epidemia podría estar entre unos 9500 y unos 12800 según la horquilla marcada por los dos modelos considerados.
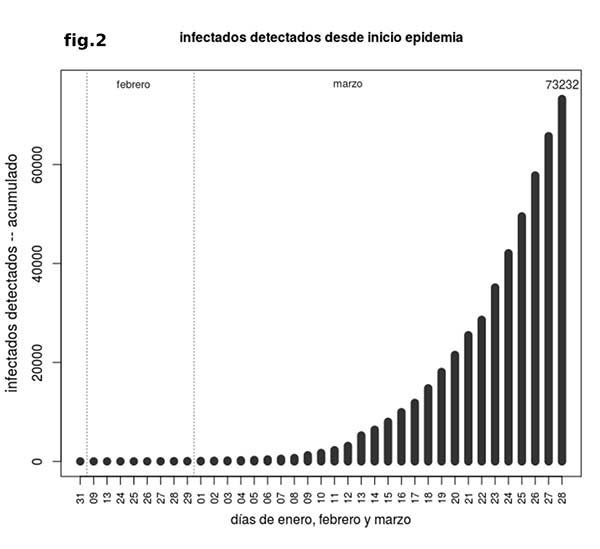
Hay que tener en cuenta que el número de casos detectados ha de ser bastante inferior al número real total en cada momento ya que, en España, solo se está informando de casos detectados directamente por test virológico (en China, por ejemplo, a partir de un determinado momento se empezó a contabilizar casos por sintomatología clínica, sin test). Según algunos estudios la cifra real podría ser tan alta como 10 veces el número de detectados, la mayoría de ellos asintomáticos, aunque posiblemente con capacidad para transmitir la enfermedad. Esto tiene varias implicaciones, tanto desde el punto de vista de la gestión para evitar la propagación del virus, como a la hora de comprender los números de los que se dispone. Por ejemplo, la mortalidad tan alta del 8% sobre casos detectados será mucho más baja si se considera el total de infectados reales, bajando al 0.8% si esa relación 10 a 1 es correcta. Esto no importa a efectos de cálculo de datos en los mismos términos que los disponibles y para las proyecciones de, por ejemplo, el momento en el que se acabará la epidemia.
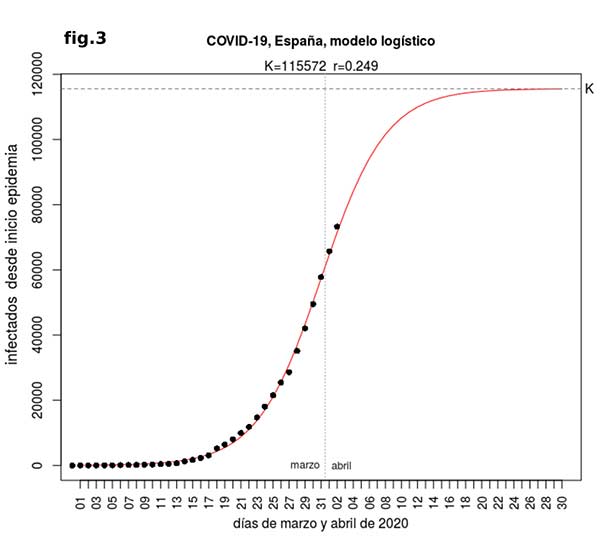
En cuanto a la duración de la epidemia, una vez que podemos estimar K es posible ajustar los datos observados a uno de los dos modelos por técnicas matemáticas de regresión y a partir de la ecuación obtenida extrapolar hacia el futuro. Cuando hacemos esto para el modelo logístico, viendo la curva de proyección resultante (fig. 3) observamos que el número de casos diarios se aproximará a cero alrededor de mediados de abril (la curva tiende a la asíntota K). En caso de ajustar a modelo de Gompertz el resultado es aproximadamente el mismo, con la diferencia de que el número de casos crece más deprisa ya que se debe llegar a una K más alta.
Hay que tener en cuenta que en ese momento no habrá 115 a 157 mil infectados activos ya que muchos habrán ido dándose de alta o fallecido. A partir de alcanzar esa K lo que ocurre es que el número de detectados desde inicio de epidemia ya no crece, a la vez que, paulatinamente, los enfermos activos van disminuyendo, sea porque se curan o sea por fallecimiento. En este momento por ejemplo, para unos 70000 casos detectados en total desde inicio de la epidemia, quedan unos 50000 activos.
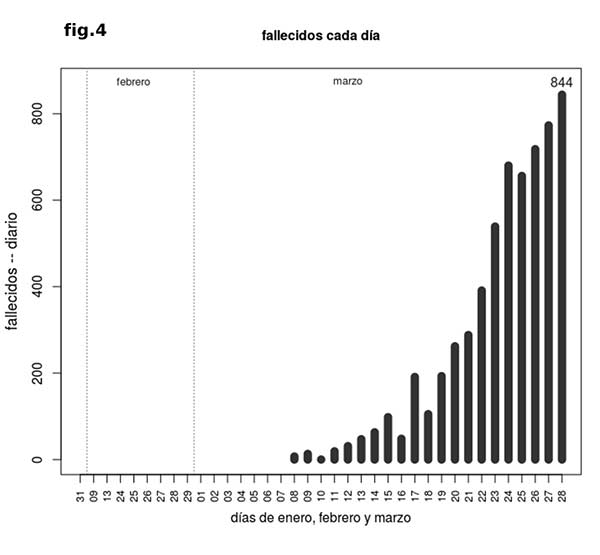
Es posible ajustar las curvas a los datos de fallecidos (fig. 4), que son más fiables, pero el problema es que desde que se detecta una infección y el momento en que, eventualmente, se produce el fallecimiento pasan varios días, por lo que el pico de fallecidos viene después del de infectados detectados. Con los datos actuales, se puede estimar una tasa diaria de unos 1000 fallecidos al día a una semana vista desde el pico de infectados aproximadamente, momento en el que la curva de fallecidos comenzaría en principio su propio camino descendente.
Julio Álvarez Jiménez, 29/03/2020














